The ROle of black holes in Star cluster dynamics
|
Globular clusters are old stellar systems containing hundreds of thousands to millions of stars. Globular clusters are observed in all galaxy types: the Milky Way contains approximately 150 observed globular clusters and large elliptical galaxies like M87 can contain 10,000 or more. Unlike the Galactic field, where individual stars and binaries essentially evolve as isolated systems due to the low densities of this environment, globular clusters are dense environments where gravitational interactions between stars are common. For a typical cluster with roughly a millions stars at birth and a standard initial mass function (e.g., Kroupa 2001), of order 1000 black holes are expected to form at early times. Once formed, these black holes congregate in their host clusters’ dense cores due to mass segregation. Within these central regions, the effect of dynamical encounters on the subsequent lives of the black holes becomes especially pronounced.
|
Figure 1: Milky Way globular cluster M15 (Credit: NASA/ESA)
|
Exploring the dynamics of stellar-mass black holes in dense star clusters like globular clusters is a key theme of my work. This topic has seen a boom in interest over the past decade. On the observational side, a growing number of stellar-mass black hole candidates have been observed in Milky Way globular clusters through both radial velocity measurements (Giesers et al. 2018, 2019) and through X-ray/radio observations (Strader et al. 2012; Chomiuk et al. 2013; Miller-Jones et al. 2015; Shishkovsky et al. 2018). On the theoretical side, state-of-the-art N-body modelling has shown that stellar-mass black holes form and are retained in stellar clusters of all masses (e.g., Morscher et al. 2015; Wang et al. 2015; Rodriguez et al. 2016; Banerjee 2017; Askar et al. 2018; Arca Sedda et al. 2018; Kremer et al. 2020a; Weatherford et al. 2019). Furthermore, cluster simulations have revealed that these black holes play a crucial role in the long- term dynamics, core evolution, and survival of stellar clusters (e.g., Mackey et al. 2007; Breen & Heggie 2013; Chatterjee et al. 2017; Kremer et al. 2018b; Ye et al. 2019; Kremer et al. 2019a; Giersz et al. 2019; Kremer et al. 2020a; Wang 2020).
|
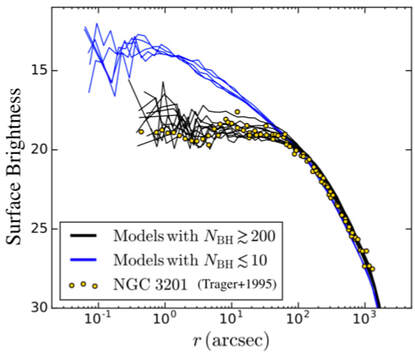
Figure 2: Adapted from Kremer et al. 2018b. Present-day surface brightness profiles for a set of N-body GC models compared to observed profile for NGC 3201 (yellow circles; data from Trager et al. 1995). Black curves show models retaining >200 black holes at late times and blue curves show (core-collapsed) models retaining <10 black holes. The differences between these models can be attributed to the ``black hole burning'' dynamical process.
|
A key result of my recent work has been demonstration of the crucial role black holes play in the long-term dynamics, core evolution, and survival of stellar clusters. In 2018 (in response to the black hole candidate announced in the Milky Way cluster NGC 3201 by the MUSE survey; Giesers et al. 2018), my team and I produced the first realistic N-body models of NGC 3201 that included stellar-mass black holes (Kremer et al. 2018b) and demonstrated that clusters like NGC 3201 with large observed core radii must retain large populations of black holes at present to explain their observed properties (see Figure 2). These models also naturally show the dynamical processes through which black hole binaries (similar to the MUSE detection) can form. Following my theoretical work on NGC 3201, the MUSE survey team identified two additional black hole candidates in this cluster (Giesers et al. 2019).
Milky Way clusters exhibit a well-observed bimodal distribution in core radii separating core-collapsed and non-core-collapsed clusters. Explaining this bimodality, and specifically explaining why, in spite of their short relaxation times, most globular clusters are not core collapsed, has been a major puzzle in stellar dynamics |
for nearly half a century. In Kremer et al. 2019a, we showed that the distinction between core-collapsed and non-core-collapsed clusters can be naturally explained by black hole dynamics. While a large number of black holes are retained in a cluster, the cluster exhibits a large observed core radius due to energy generated through ``black hole burning.'' Only when a cluster's black hole population has been almost fully depleted can a cluster attain a core-collapsed architecture. Furthermore, we showed that a cluster's initial size (as motivated by observations of young massive clusters; Portegies Zwart et al. 2010) determines the number of black holes retained and, ultimately, the core-collapse process.
Most recently, in Kremer et al, (2020a), we developed a public catalog of roughly 1000 N-body cluster models that cover nearly completely the parameter space exhibited by the observed globular clusters in the Milky Way, enabling a detailed exploration of the role of ``black hole burning'' across all globular cluster types. Overall, my computational work has been a key complement to the growing number of observed black hole candidates in clusters, demonstrating that black holes are indeed present and dynamically significant throughout the full lifetimes of realistic clusters.
Modeling globular clusters is a computationally challenging endeavor (e.g., Heggie & Hut 2003). My collaborators and I use the Cluster Monte Carlo code CMC (for a review, see Rodriguez et al. 2022) to model these systems. CMC includes all physics relevant for studying the formation and evolution of compact objects in dense star clusters including two-body relaxation, direct integration of small-N encounters, and stellar/binary evolution using the COSMIC population synthesis code.
Most recently, in Kremer et al, (2020a), we developed a public catalog of roughly 1000 N-body cluster models that cover nearly completely the parameter space exhibited by the observed globular clusters in the Milky Way, enabling a detailed exploration of the role of ``black hole burning'' across all globular cluster types. Overall, my computational work has been a key complement to the growing number of observed black hole candidates in clusters, demonstrating that black holes are indeed present and dynamically significant throughout the full lifetimes of realistic clusters.
Modeling globular clusters is a computationally challenging endeavor (e.g., Heggie & Hut 2003). My collaborators and I use the Cluster Monte Carlo code CMC (for a review, see Rodriguez et al. 2022) to model these systems. CMC includes all physics relevant for studying the formation and evolution of compact objects in dense star clusters including two-body relaxation, direct integration of small-N encounters, and stellar/binary evolution using the COSMIC population synthesis code.